publié le 20 fév 2017 par Hélène HORSIN MOLINARO [1]
Contenu principal
Contenus associés :
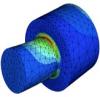
Cette ressource explique quelles sont les propriétés géométriques et cinématiques des éléments finis et les illustre sur quelques types d'éléments usuels
Ressource pédagogique
Auteur(s):
GENDRE Lionel [7]
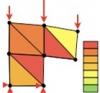
Cette ressource illustre la convergence sur un exemple simple, et en déduit quelques principes visant à raffiner les maillages de façon pertinente en optimisant le rapport entre précision des résultats et coût de la simulation
Ressource pédagogique
Auteur(s):
GENDRE Lionel [7]
Cette ressource explique ce qu’est une singularité et montre, exemples à l'appui, quelles sont les erreurs y conduisant et comment les éviter
Ressource pédagogique
Auteur(s):
GENDRE Lionel [7]